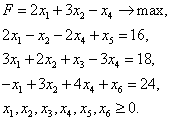Симплекс метод в курсовом проекте на С++ основные принципы и примеры

В данной статье рассмотрим использование симплекс метода в курсовом проекте на языке программирования С++. Симплекс метод — эффективный инструмент для решения задач линейного программирования, основанный на последовательном улучшении плана. Основная идея метода заключается в переходе от текущего плана к новому плану с более высоким значением целевой функции-цели.

Для обеспечения работы алгоритма симплекс метода в курсовом проекте используются такие структуры данных, как массив и кортеж (tuple), а также матрица, содержащая коэффициенты системы ограничений и значений целевой функции-цели.

В нашем примере решается задача минимизации, поставленная перед пользователем. Данные для решения задачи хранятся в массиве, содержащем индексную информацию, а также базисные переменные и их значения. Весь процесс заполнения и обработки данных производится при помощи функций и методов языка программирования С++. В результате работы алгоритма мы сможем вывести на экран ответ — оптимальный план и значение целевой функции-цели.

Постановка задачи

Для реализации противоположного (обратного) процесса в программе создается массив, который будет хранить индексы входящих в базисные переменные. Затем, в цикле по каждой итерации алгоритма, массив заполняется индексами элементов столбца разрешающего элемента, который выбирается на каждой итерации.

Первым шагом разработка проекта состоит в вводе данных, таких как размеры таблицы и коэффициенты ограничений. Перед вводом размеров таблицы пользователь вводит номер основной переменной, а затем вводит первую строку таблицы. Ввод осуществляется с помощью функции create, которая создает объект типа std::stringstream, и функции getline, которая считывает строку из стандартного ввода. Затем функция create вызывает функцию split, которая разделяет строку на значения и помещает их в вектор.

Разработка алгоритма программы

Для решения задачи линейного программирования в курсовой проекте на языке программирования C++ можно использовать симплекс-метод. Данный алгоритм основан на поиске оптимального решения задачи, которое достигается при определенных значениях переменных.

Вначале необходимо создать таблицу симплекс-метода, которая будет содержать все данные по заданной задаче: коэффициенты целевой функции, условия и ограничения. Элементы таблицы будут представлять собой числа, которые зависят от индексов столбца и строки. Первый столбец таблицы содержит коэффициенты функции-цели, а строки — значения базисных переменных. Элементы первой строки таблицы могут быть массивом, содержащим коэффициенты переменных системы ограничений.

Дальше алгоритм проходит через итерации, в которых происходит вычисление разрешающего элемента с использованием простых математических операций (сложение, вычитание, умножение и деление). В каждой итерации проверяется, есть ли возможность улучшить решение задачи, и если это возможно, то происходит переход к следующей итерации.

Приведенный ниже пример кода на языке C++ демонстрирует основные шаги алгоритма симплекс-метода:

#include <iostream>
#include <vector>
#include <sstream>
#include <stdexcept>
using namespace std;
void printArray(vector<vector<double>>& arr) {
for (int i = 0; i < arr.size(); i++) {
for (int j = 0; j < arr[i].size(); j++) {
cout << arr[i][j] << " ";
}
cout << endl;
}
}
// Функция для поиска разрешающего элемента
vector<int> findPivot(vector<vector<double>>& arr) {
int numRows = arr.size();
int numCols = arr[0].size();
int minRow = 1, minCol = 0;
double minValue = arr[minRow][minCol];
for (int i = 1; i < numRows - 1; i++) {
if (arr[i][minCol] > 0) {
double ratio = arr[i][numCols - 1] / arr[i][minCol];
if (ratio < minValue) {
minValue = ratio;
minRow = i;
}
}
}
vector<int> pivot = {minRow, minCol};
return pivot;
}
// Функция для обновления таблицы
void updateTable(vector<vector<double>>& arr, vector<int>& pivot) {
int numRows = arr.size();
int numCols = arr[0].size();
int pivotRow = pivot[0];
int pivotCol = pivot[1];
double pivotValue = arr[pivotRow][pivotCol];
for (int i = 0; i < numCols; i++) {
arr[pivotRow][i] /= pivotValue;
}
for (int i = 0; i < numRows; i++) {
if (i != pivotRow) {
double factor = -arr[i][pivotCol];
for (int j = 0; j < numCols; j++) {
arr[i][j] += factor * arr[pivotRow][j];
}
}
}
}
// Главная функция алгоритма симплекс-метода
void simplexMethod(vector<vector<double>>& arr) {
int numRows = arr.size();
int numCols = arr[0].size();
while (true) {
vector<int> pivot = findPivot(arr);
int pivotRow = pivot[0];
int pivotCol = pivot[1];
if (arr[pivotRow][pivotCol] <= 0) {
break;
}
updateTable(arr, pivot);
}
}
int main() {
// Создание таблицы симплекс-метода
vector<vector<double>> table = {
{4, -5,  0,  1,  0,  0, 75},
{6, -8,  0,  0,  1,  0, 96},
{3,  2, -1,  0,  0,  1, 36}
};
// Вызов функции симплекс-метода
simplexMethod(table);
cout << "Результат: " << table[numRows - 1][numCols - 1] << endl;
return 0;
}

В данном примере рассмотрен случай постановки задачи на минимум функции-цели. Но алгоритм также может быть адаптирован для решения задачи на максимум.

Таким образом, разработка алгоритма программы на языке C++ для решения задачи линейного программирования с использованием симплекс-метода может быть выполнена с помощью описанных выше шагов и примера кода.

Математическое обеспечение

Разработка алгоритма симплекс-метода

Перед разработкой алгоритма симплекс-метода необходимо учесть задачу линейного программирования, поставленную в курсовой работе. Цель данной задачи — максимизировать целевую функцию при заданных ограничениях.

Постановка задачи

Для разработки алгоритма симплекс-метода необходимо сформулировать задачу линейного программирования в виде системы уравнений и неравенств. Данная система включает в себя коэффициенты целевой функции и ограничения, представленные в виде матрицы коэффициентов при переменных.

Разрешающий элемент

Разрешающий элемент выбирается путем поиска минимального значения по строке с отрицательным коэффициентом перед переменной. Это элемент, который будет вводиться в базис и станет основой для следующего шага алгоритма.

Пересчет

Пересчет производится путем деления элементов строки с разрешающим элементом на значение разрешающего элемента. Таким образом, все коэффициенты строки будут приведены к 1. Затем, с помощью элементарных операций над строками матрицы, все остальные элементы в столбце и строке разрешающего элемента обнуляются. Таким образом, матрица постепенно преобразуется к оптимальному решению задачи.

Ограничения и целевая функция

Ввод данных ограничений и коэффициентов целевой функции осуществляется с помощью пользовательского ввода. Первая строка массива данных содержит целевую функцию, а последующие строки содержат ограничения задачи. Каждый элемент матрицы представлен в виде числа, которое может быть со знаком + или -.

Обработка ошибок

В случае возникновения ошибки, связанной с неправильным вводом данных или матрицы симплекс-метода, вызывается исключение. Данный механизм обработки ошибок помогает предотвратить некорректное выполнение алгоритма и сообщить пользователю о возникшем недостатке данных.

Видео:

СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

СИМПЛЕКС МЕТОД: ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ by Наталия Назаренко 79,018 views 3 years ago 19 minutes